Maple计算器高级版

软件介绍

Maple计算器高级版是一款好用的在线数学计算软件，一款能够让每一个用户都能在软件中一站式体验最简单的数据方程输入方式，专为每一个用户带来最简单的在线数学公式使用。Maple计算器高级版破解版内置了全网最好用的在线方程一键分析功能，用户在这里数据方程公式，智能解析，专为每一个学习数学的用户带来便捷的解析方式，让你的学习更容易。

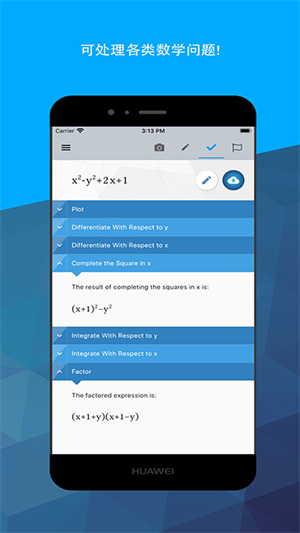
Maple计算器高级版app提供了全新的图形化数据问题分析和解答功能，用户能够在这里一站式创建数学图形，最全的在线解析，最全的公式解答，让每一个用户都能在软件中完成数据解析。

软件特色

1、 基本运算：算数、分数、小数、整数、因数、平方根、幂运算。

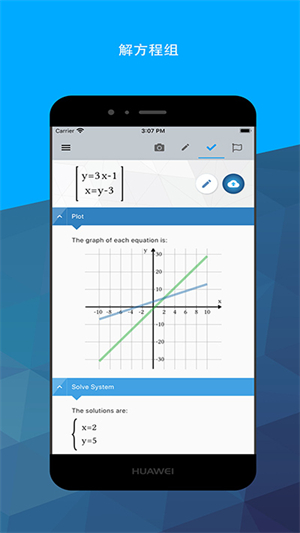
2、代数：线性方程组求解和绘图、方程组求解与绘图、处理多项式、二次方程与二次函数、对数函数与指数函数、三角函数、三角恒等式。

3、预科微积分：图形、分段函数、绝对值、不等式、隐函数。

软件亮点

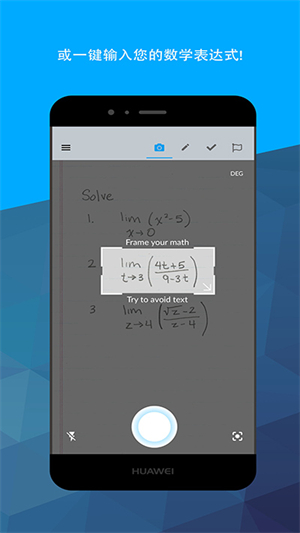
1、只需单击即可输入算式：在相机上一键单击即可使用功能强大的人工智能技术，输入手写和排印的数学问题。或者，使用与您老师一样的数学符号，在计算器中输入数学表达式——问题输入非常轻松，因为它“看上去很顺眼”！

2、进行各种数学运算：无论通过何种方式输入数学问题，您都能求出导数和积分、解系数多项式、矩阵求逆、解方程组、解常微分方程等等。这款应用有世界领先的Maple数学引擎强大的功能作为后盾，可以完成海量的数学运算！

3、获得详细解题步骤：除了答案之外，还可以得到各种数学题的完整解题步骤，包括解方程组、求极限/导数/积分、完成矩阵运算等等！

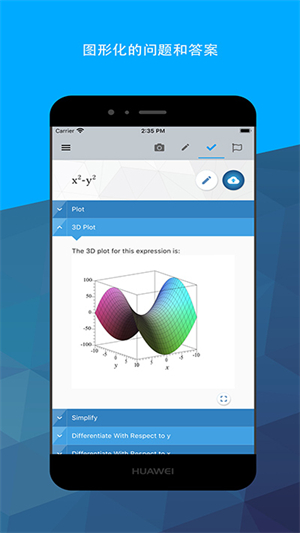
4、图形问题求解：即刻查看表达式的二维和三维图形，观看改写表达式时图形会如何变化。您可以放大、平移甚至旋转三维图，以更仔细查看求解区域。

5、您离线时也能求解：应用的某些功能需要连接互联网，但您可随时使用图形计算器！

6、将计算结果直接上传到Maple Learn：使用相机将手写步骤自动发送到Maple Learn，您可以在其中发现错误并与他人分享您的工作。

7、避免在使用Maple桌面版时的转写错误：避免在向Maple转写数学表达式时可能出现的错误，使用应用拍照并将结果上传至Maple，即可进行进一步探究和可视化。

8、支持国际语言：提供英语、西班牙语、法语、德语、俄语、丹麦语、瑞典语、日语和简体中文。

怎么用

1、首先打开maple计算器手机版。

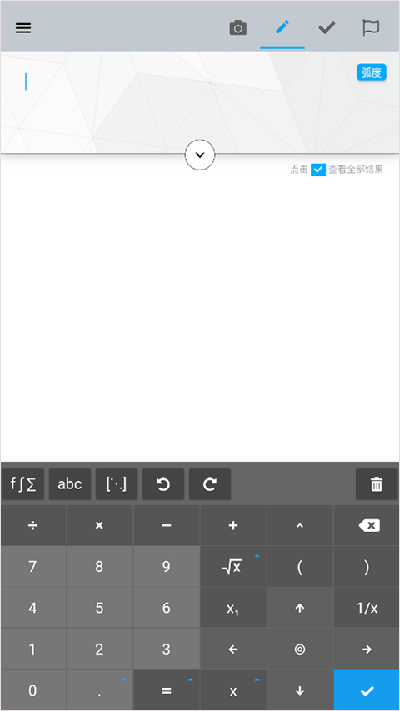
2、你可以随意输入公式、方程式等，可以清晰的查看到结果。

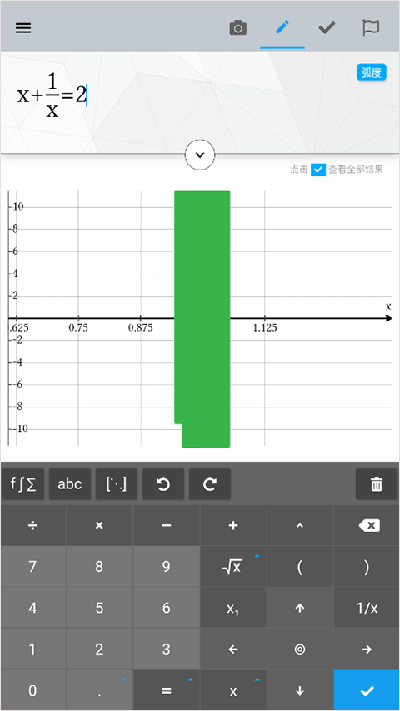
3、还可以输入复杂的方程式，也能自动显示计算的结果。

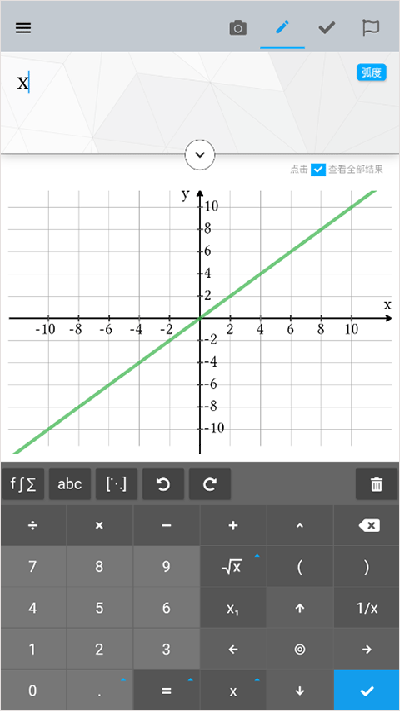
4、点击右上方按钮，还可以查看到方程两边的图。

5、求解x、化简、求微分等功能，非常好用。

适用的领域

1、金融建模：金融函数包提供大量的工具用于高级金融建模，包括个人理财工具，适用于风险分析、证券管理、定量分析、和模型验证领域，Maple其包含的大量函数命令，能够解决模型的构建和计算问题。

2、物理领域：Maple中的大量函数和特殊函数工具，能够解决物理领域的函数计算，包括经典力学、量子力学、张量计算、计算常微分方程和偏微分方程的封闭解、抽象矢量代数、特殊函数、电动力学。

3、信号处理：Maple之中存在信号处理工具，可用于分析和处理频域和时域中的数据，被应用于通信、滤波器设计、振动和噪音衰减、数字信号处理应用。

4、控制和设计：Maple中所包含的函数包提供了大量的数值和符号算法，用于数据处理和可视化。Maple工具包提供大量的工具实现控制对象建模和高级控制系统设计。

怎么打平方

1、首先输入数字，然后点击图中的平方号。

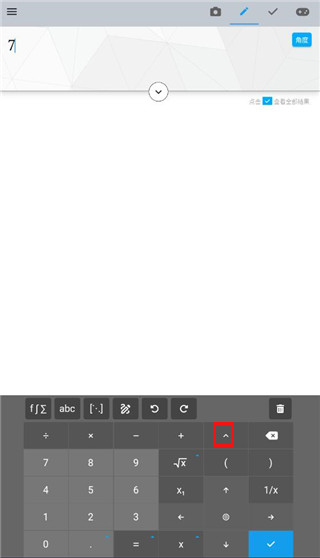
2、这样这个数的平方就即算出来了。

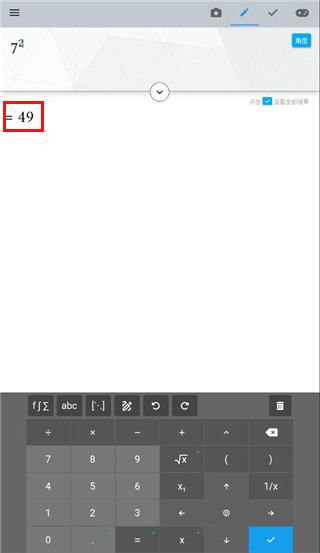
3、点击左上角的科学符号，还可以展开更多的数学符号。

4、点击英文字母可以调出26个字母。

5、当打出x的平方时，还可以绘制出x二次方的函数图。

解方程组

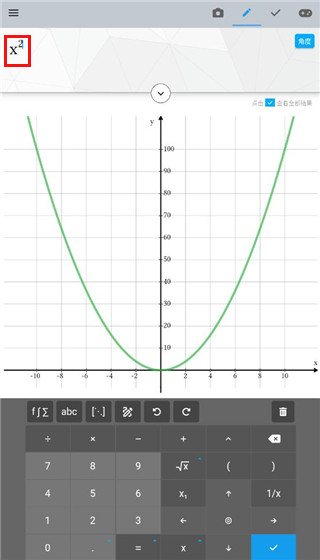
1、打开Maple，定义需要求解的方程组，如果输入的是矩阵形式，先将矩阵化成方程，输入方程组的系数矩阵A，点击回车，如下：

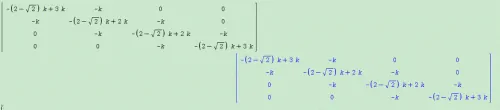
2、将方程写成[A]*[X]=0的形式，点击回车得到非矩阵形式的线性方程组，如下：

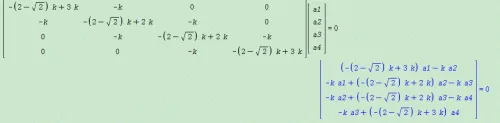
3、如上图，我们得到4个方程，现在将方程分开写成。

（1）eqn1:=方程1=0；

（2）eqn2:=方程2=0；

（3）eqn3:=方程3=0；

（4）eqn4:=方程4=0；

具体，如下图表示：

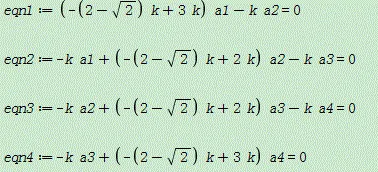
4、输入命令语句：solve（{eqn1，eqn2，eqn3，eqn4}，{a1,a2,a3,a4}）：

这里第一个“{}”中写需要求解的方程编号，第二个“{}”中写求解的变量，点击回车：